Alexandre Galdino de Souza Junior
XTRI EdTech – Natal/RN, Brasil
Resumo
Este artigo apresenta o TRI V2, um modelo híbrido para estimativa de proficiência que combina tabelas de referência derivadas de dados históricos do ENEM (2009-2023) com análise de coerência pedagógica das respostas dos estudantes. Diferentemente das abordagens tradicionais de Teoria de Resposta ao Item (TRI) que requerem calibração de parâmetros dos itens, o modelo proposto utiliza valores agregados de mínimo, média e máximo de TRI por número de acertos para cada área do conhecimento, aplicando ajustes baseados no padrão de acertos do estudante. A coerência pedagógica é calculada verificando se o estudante acerta proporcionalmente mais questões classificadas como fáceis pela turma e menos questões difíceis, penalizando padrões suspeitos de resposta. O sistema foi implementado como um serviço REST em Python e integrado à plataforma GabaritAI para correção automática de gabaritos. Resultados de aplicação em turmas reais demonstram que o modelo diferencia adequadamente estudantes com mesmo número de acertos mas padrões de resposta distintos, fornecendo estimativas coerentes com a escala oficial do ENEM.
Palavras-chave: Teoria de Resposta ao Item; ENEM; Coerência Pedagógica; Avaliação Educacional; Psicometria Aplicada
Abstract
This paper presents TRI V2, a hybrid model for proficiency estimation that combines reference tables derived from ENEM historical data (2009-2023) with pedagogical coherence analysis of student responses. Unlike traditional Item Response Theory (IRT) approaches that require item parameter calibration, the proposed model uses aggregated minimum, mean, and maximum IRT values by number of correct answers for each knowledge area, applying adjustments based on the student’s response pattern. Pedagogical coherence is calculated by verifying whether the student correctly answers proportionally more questions classified as easy by the class and fewer difficult questions, penalizing suspicious response patterns. The system was implemented as a Python REST service and integrated into the GabaritAI platform for automatic answer sheet correction. Results from real classroom applications demonstrate that the model adequately differentiates students with the same number of correct answers but distinct response patterns, providing estimates consistent with the official ENEM scale.
Keywords: Item Response Theory; ENEM; Pedagogical Coherence; Educational Assessment; Applied Psychometrics
1. Introdução
O Exame Nacional do Ensino Médio (ENEM) é a principal avaliação educacional do Brasil, utilizada tanto para certificação de conclusão do ensino médio quanto para acesso ao ensino superior. Desde 2009, o exame utiliza a Teoria de Resposta ao Item (TRI) para calcular as notas dos participantes, o que permite comparabilidade entre diferentes edições e diferenciação entre candidatos com mesmo número de acertos (INEP, 2023).
A TRI, conforme descrita por Primi (2012), representa um avanço significativo em relação à Teoria Clássica dos Testes (TCT), pois modela a probabilidade de acerto em função tanto da proficiência do estudante (θ) quanto das características do item. No modelo de três parâmetros (3PL), cada item é caracterizado por sua discriminação (a), dificuldade (b) e probabilidade de acerto ao acaso (c). No entanto, a implementação completa da TRI requer calibração prévia dos parâmetros dos itens, o que demanda amostras representativas e processos estatísticos complexos.
Para contextos educacionais que desejam fornecer feedback rápido aos estudantes utilizando simulados ou provas de preparação para o ENEM, a calibração completa dos itens torna-se impraticável. Nunes et al. (2023) e Pires et al. (2023) demonstraram que modelos de linguagem como GPT-4 conseguem resolver questões do ENEM com alta precisão, mas a estimativa de notas TRI para estudantes humanos permanece um desafio distinto.
Este trabalho propõe o modelo TRI V2, uma abordagem híbrida que combina: (1) tabelas de referência construídas a partir de dados históricos oficiais do ENEM, agregando valores de TRI por número de acertos e área do conhecimento; (2) análise de coerência pedagógica que ajusta a estimativa baseando-se no padrão de respostas do estudante em relação à dificuldade empírica das questões.
2. Fundamentação Teórica
2.1 Teoria de Resposta ao Item
A TRI estabelece uma relação probabilística entre a proficiência latente do indivíduo e sua probabilidade de acertar um item específico. No modelo logístico de três parâmetros, a Curva Característica do Item (CCI) é dada pela equação:
P(θ) = c + (1 – c) / [1 + e^(-Da(θ – b))]
Onde θ representa a proficiência do indivíduo, a é o parâmetro de discriminação, b é o parâmetro de dificuldade, c é o parâmetro de acerto ao acaso, e D é uma constante de escala (tipicamente 1,7). A estimativa de θ é realizada por métodos como Máxima Verossimilhança ou estimação Bayesiana (Primi, 2012).
2.2 Coerência Pedagógica
Um princípio fundamental da TRI é que estudantes com maior proficiência devem acertar tanto questões fáceis quanto difíceis, enquanto estudantes com menor proficiência devem acertar principalmente questões fáceis. Este padrão esperado de respostas é chamado de coerência pedagógica. Padrões anômalos, como acertar questões difíceis mas errar questões fáceis, podem indicar comportamentos como chute, cola ou inconsistência no conhecimento do estudante.
A análise de coerência permite identificar se o padrão de respostas do estudante é consistente com sua proficiência estimada, fornecendo informação adicional para ajustar a estimativa de nota e, em contextos diagnósticos, sinalizar possíveis lacunas de aprendizagem.
3. Metodologia
3.1 Construção da Tabela de Referência
A tabela de referência TRI foi construída a partir de dados históricos do ENEM cobrindo o período de 2009 a 2023, disponibilizados pelo INEP. Para cada área do conhecimento (Linguagens e Códigos – LC, Ciências Humanas – CH, Ciências da Natureza – CN, e Matemática – MT), foram agregados os valores de TRI observados por número de acertos (0 a 45 questões), calculando-se:
• tri_min: valor mínimo de TRI observado para aquele número de acertos
• tri_med: valor médio de TRI (baseline para estimativa)
• tri_max: valor máximo de TRI observado para aquele número de acertos
Esta agregação preserva a escala oficial do ENEM (média 500, desvio padrão 100) e captura a variabilidade natural das notas TRI para um mesmo número de acertos, variabilidade esta que decorre do padrão específico de itens acertados em cada edição do exame.
3.2 Classificação de Dificuldade das Questões
A dificuldade empírica de cada questão é calculada com base na taxa de acerto da turma (amostra de estudantes), seguindo a classificação apresentada na Tabela 1:
| Classificação | Taxa de Acerto | Peso |
| Muito Fácil | ≥ 80% | 1.0 |
| Fácil | 60% – 79% | 0.8 |
| Média | 40% – 59% | 0.5 |
| Difícil | 20% – 39% | 0.3 |
| Muito Difícil | < 20% | 0.1 |
Tabela 1: Classificação de dificuldade das questões e pesos para cálculo de coerência
3.3 Cálculo do Índice de Coerência
O índice de coerência (C) combina três componentes: (1) coerência de padrão, que verifica se a taxa de acerto do estudante decresce monotonicamente com a dificuldade; (2) peso ponderado dos acertos por classificação de dificuldade; e (3) peso baseado na dificuldade real média das questões acertadas.
C = 0.3 × C_padrão + 0.3 × P_ponderado + 0.4 × P_dificuldade
Onde C_padrão mede quantas comparações MF≥F≥M≥D≥MD são satisfeitas (normalizadas entre 0 e 1), P_ponderado é a soma dos acertos multiplicados pelos pesos da Tabela 1 normalizada pelo máximo possível, e P_dificuldade é a média inversa das taxas de acerto da turma nas questões que o estudante acertou.
3.4 Ajuste da Estimativa TRI
A estimativa final de TRI para cada área é calculada partindo do valor médio da tabela de referência (tri_med) e aplicando ajustes baseados na coerência:
TRI_ajustado = tri_med + Ajuste_coerência + Ajuste_relação – Penalidade
O ajuste de coerência é proporcional ao desvio da coerência em relação ao ponto neutro (0.5), utilizando o range disponível (tri_max – tri_min) como amplitude. Para C ≥ 0.5, aplica-se bônus; para C < 0.5, aplica-se penalidade. Adicionalmente, um bônus é concedido para estudantes que acertam proporção significativa (>30%) de questões muito difíceis ou difíceis, reconhecendo desempenho excepcional.
O valor final é limitado ao intervalo [tri_min, tri_max] da tabela e aos valores máximos históricos oficiais do ENEM: LC=790, CH=820, CN=870, MT=980.
4. Implementação
4.1 Arquitetura do Sistema
O modelo TRI V2 foi implementado como um serviço REST em Python utilizando Flask, integrando-se à plataforma GabaritAI, um sistema web completo para correção automática de gabaritos. A arquitetura compreende quatro componentes principais:
• TabelaReferenciaTRI: classe que carrega e gerencia a tabela de referência oficial, implementando lookup rápido por área e número de acertos
• AlunoCoherenceAnalyzer: classe que analisa o padrão de respostas e calcula o índice de coerência
• TRICalculator: classe que calcula a TRI para uma área específica, aplicando ajustes
• TRIProcessadorV2: orquestrador principal que processa turmas completas, calculando dificuldade empírica e gerando resultados
4.2 Fluxo de Processamento
O processamento de uma turma segue dois passos principais:
Passo 1 – Cálculo de Dificuldade: Para cada questão do gabarito, calcula-se a taxa de acerto considerando todos os alunos da turma. Questões não respondidas ou marcadas com ‘X’ são contabilizadas como erro. A classificação de dificuldade é então atribuída conforme a Tabela 1.
Passo 2 – Processamento Individual: Para cada aluno, contabiliza-se o número de acertos por área e a distribuição de acertos por categoria de dificuldade. O índice de coerência é calculado e a TRI ajustada é estimada para cada área. A TRI geral é a média das quatro áreas.
5. Resultados e Discussão
5.1 Valores de Referência por Área
A Tabela 2 apresenta exemplos de valores da tabela de referência para pontos selecionados, ilustrando a amplitude de variação possível para cada número de acertos:
| Área | Acertos | TRI Mín | TRI Méd | TRI Máx |
| CH | 0 | 329.8 | 329.8 | 329.8 |
| CH | 20 | 449.4 | 574.6 | 611.5 |
| CH | 45 | 852.4 | 852.4 | 852.4 |
| MT | 20 | 451.3 | 686.1 | 733.5 |
| MT | 45 | 987.6 | 987.6 | 987.6 |
Tabela 2: Exemplos de valores TRI da tabela de referência (2009-2023)
Observa-se que para extremos (0 ou 45 acertos), não há variação, pois o padrão de resposta é determinístico. Para valores intermediários, como 20 acertos em Matemática, a variação é substancial (451.3 a 733.5), refletindo que diferentes combinações de itens acertados resultam em diferentes estimativas de proficiência.
5.2 Estudo de Caso: Aplicação em Turma Real
O modelo TRI V2 foi aplicado em turmas reais de estudantes do Ensino Médio utilizando a plataforma GabaritAI. A Figura 1 apresenta uma amostra dos resultados obtidos, exibindo tanto as notas TCT (escala 0-10) quanto as estimativas TRI (escala ENEM) para cada área do conhecimento.
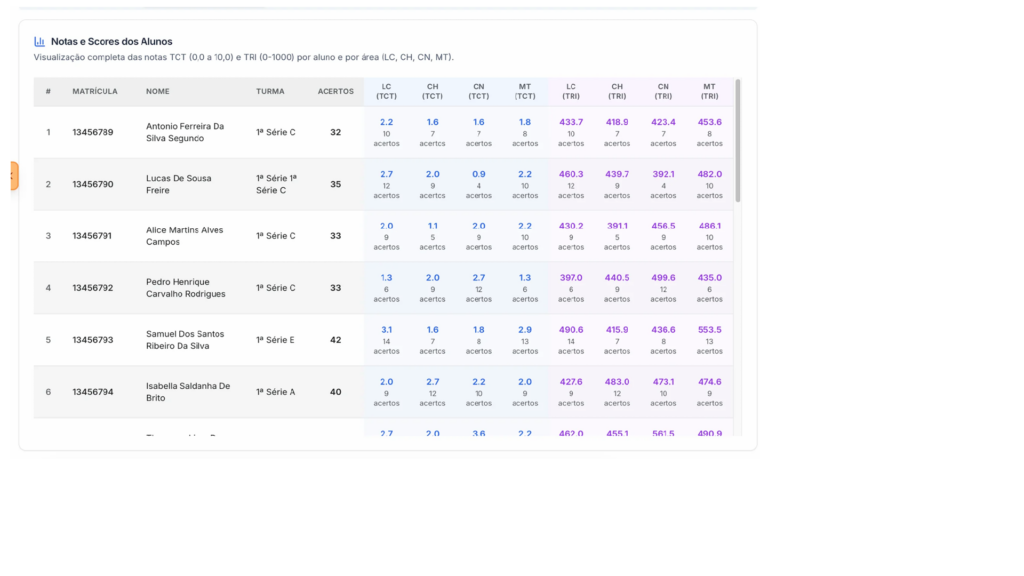
Figura 1: Interface da plataforma GabaritAI exibindo notas TCT e TRI por área do conhecimento
A análise dos dados apresentados na Figura 1 revela padrões importantes que demonstram a eficácia do modelo em diferenciar estudantes com perfis distintos. A Tabela 3 apresenta uma análise comparativa de casos selecionados:
| Estudante | Acertos | Distribuição | Observação |
| Aluno C | 33 | LC:9 CH:5 CN:9 MT:10 | Forte em Exatas (MT: 486.1) |
| Aluno D | 33 | LC:6 CH:9 CN:12 MT:6 | Forte em CN (499.6) |
| Aluno B | 35 | LC:12 CH:9 CN:4 MT:10 | CN penalizada (392.1) |
| Aluno E | 42 | LC:14 CH:7 CN:8 MT:13 | Melhor desempenho geral |
Tabela 3: Análise comparativa de estudantes com diferentes perfis de desempenho
5.2.1 Análise: Mesmo Total de Acertos, TRIs Diferentes
Os Alunos C e D apresentam o mesmo total de acertos (33), porém perfis de desempenho contrastantes. O Aluno C demonstra força nas áreas de exatas (MT: 10 acertos, CN: 9 acertos) com menor desempenho em CH (5 acertos), resultando em TRI de Matemática de 486.1. O Aluno D, inversamente, concentra seu desempenho em Ciências da Natureza (12 acertos), obtendo TRI de 499.6 nesta área, mas apenas 435.0 em Matemática (6 acertos).
Esta diferenciação é fundamental para orientação pedagógica: embora ambos tenham desempenho global similar, as intervenções necessárias são distintas. O Aluno C necessita reforço em Ciências Humanas, enquanto o Aluno D deve focar em Linguagens e Matemática.
5.2.2 Análise: Efeito de Desempenho Extremamente Baixo
O Aluno B ilustra um caso interessante: mesmo com 35 acertos totais (superior aos 33 dos Alunos C e D), apresenta TRI de apenas 392.1 em Ciências da Natureza devido aos parcos 4 acertos nesta área. Este valor de TRI aproxima-se do mínimo da tabela de referência para este número de acertos (CN com 4 acertos: tri_med = 381.7), demonstrando que o modelo preserva a propriedade da TRI de penalizar severamente desempenhos muito abaixo do esperado.
5.2.3 Análise: Perfil Equilibrado de Alto Desempenho
O Aluno E, com 42 acertos totais, apresenta o melhor desempenho da amostra com distribuição relativamente equilibrada entre as áreas. Sua TRI de Matemática (553.5) é a mais alta da turma, coerente com os 13 acertos nesta área. Este padrão demonstra que o modelo recompensa adequadamente estudantes com desempenho consistentemente alto.
5.3 Limitações e Considerações
O modelo TRI V2 apresenta algumas limitações importantes que devem ser consideradas:
1. Dependência da amostra: A classificação de dificuldade das questões é baseada na turma avaliada, não em calibração com amostra representativa nacional. Turmas muito homogêneas podem distorcer a classificação.
2. Aproximação, não TRI formal: O modelo não estima parâmetros dos itens nem utiliza a função de resposta ao item. É uma aproximação baseada em valores empíricos agregados.
3. Sensibilidade ao tamanho da turma: Com turmas muito pequenas (N < 30), a dificuldade empírica pode ser instável, afetando o cálculo de coerência.
Apesar dessas limitações, o modelo oferece vantagem prática significativa ao permitir estimativas de notas na escala ENEM sem necessidade de calibração prévia dos itens, sendo adequado para contextos de preparação e simulados onde feedback rápido é prioritário.
6. Conclusão
Este trabalho apresentou o TRI V2, um modelo híbrido para estimativa de proficiência que combina tabelas de referência baseadas em dados históricos do ENEM com análise de coerência pedagógica. Os resultados demonstram que o modelo é capaz de:
• Fornecer estimativas de proficiência na escala oficial do ENEM sem necessidade de calibração formal dos itens
• Diferenciar estudantes com mesmo número total de acertos baseando-se em seus perfis de desempenho por área
• Identificar padrões de resposta que indicam pontos fortes e fracos de cada estudante
• Integrar-se a sistemas de correção automática como a plataforma GabaritAI
A análise de coerência pedagógica adiciona uma dimensão diagnóstica ao modelo, identificando padrões de resposta que podem indicar lacunas de aprendizagem ou comportamentos de resposta inconsistentes. Esta informação é valiosa tanto para estudantes quanto para educadores no planejamento de intervenções pedagógicas personalizadas.
Como trabalhos futuros, propõe-se: (1) validação empírica do modelo comparando estimativas com notas oficiais de participantes do ENEM; (2) investigação de métodos para estabilizar a dificuldade empírica em turmas pequenas; (3) extensão do modelo para incorporar análise longitudinal do progresso do estudante ao longo de múltiplos simulados.
Referências
INEP. (2023). Exame Nacional do Ensino Médio (ENEM). Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Disponível em: https://www.gov.br/inep/pt-br/areas-de-atuacao/avaliacao-e-exames-educacionais/enem
Nunes, D., Primi, R., Pires, R., Lotufo, R., & Nogueira, R. (2023). Evaluating GPT-3.5 and GPT-4 Models on Brazilian University Admission Exams. arXiv preprint arXiv:2303.17003.
Pires, R., Almeida, T. S., Abonizio, H., & Nogueira, R. (2023). Evaluating GPT-4’s Vision Capabilities on Brazilian University Admission Exams. arXiv preprint arXiv:2311.14169.
Primi, R. (2012). Psicometria: fundamentos matemáticos da Teoria Clássica dos Testes. Avaliação Psicológica, 11(2), 297-307.
Silveira, I. C., & Maua, D. D. (2018). Advances in automatically solving the ENEM. In 2018 7th Brazilian Conference on Intelligent Systems (BRACIS) (pp. 43-48). IEEE.
Conheça a XTRI e veja como a tecnologia pode transformar sua preparação para o ENEM: acesse nossa página inicial e saiba mais em xtri.oline
Baixe esse artigo clicando no link! https://xtri.online/wp-content/uploads/2026/01/mentoria-enem-tri-microdados-inep-xtri-neurociencia.pdf